Mean Value Theorem for class12

What is Mean Value Theorem?

• The Mean Value Theorem is typically abbreviated MVT.
• The MVT describes a relationship between average rate of change and instantaneous rate of change.
• Geometrically, the MVT describes a relationship between the slope of a secant line and the slope of the tangent line.
• Rolle's Theorem (from the previous lesson) is a special case of the Mean Value Theorem.
• The MVT has two hypotheses (conditions). Specifically,
  • continuity on [a,b]$[a,b]$
  • and differentiability on (a,b)$(a,b)$.
• If the two hypotheses are satisfied, then
  
  f′(c)=f(b)−f(a)b−a$f^{\prime }(c)=\frac{f(b)-f(a)}{b-a}$
  
  for some c∈(a,b)$c\in (a,b)$.

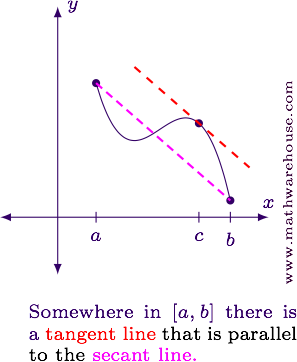
Basic Idea (Graphical)

Suppose we are looking at a function on an interval [a,b]$[a,b]$. The line connecting the endpoints (the secantline$secantline$) will be parallel to at least one of the function's tangentlines.$tangentlines.$

In order for this to be true, the function has to

Formal Statement of the Mean Value Theorem

Suppose f(x)$f(x)$ is continuous on [a,b]$[a,b]$ and differentiable on (a,b)$(a,b)$. Then there is a point at c∈(a,b)$c\in (a,b)$ where

f(b)−f(a)b−a=f′(c)$\frac{f(b)-f(a)}{b-a}=f^{\prime }(c)$

Understanding the MVT Equation

Examples of Common Questions

Example 1

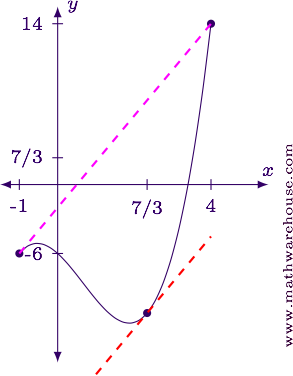
Suppose f(x)=x3−2x2−3x−6$f(x)=x^3-2x^2-3x-6$ over [−1,4]$[-1,4]$. What value of x$x$ satisfies the the Mean Value Theorem?

Step 1

Find the slope of the secant line.

f(−1)f(4)m=(−1)3−2(−1)2−3(−1)−6=−6=(4)3−2(4)2−3(4)−6=14=14−(−6)4−(−1)=205=4$\begin{array}{rl}f(-1)& =(-1{)}^3-2(-1{)}^2-3(-1)-6=-6\\ f(4)& =(4{)}^3-2(4{)}^2-3(4)-6=14\\ m& =\frac{14-(-6)}{4-(-1)}=\frac{20}{5}=4\end{array}$

Step 2

Find f′(x)$f^{\prime }(x)$.

f′(x)=3x2−4x−3$f^{\prime }(x)=3x^2-4x-3$

Step 3

Determine where f′(x)$f^{\prime }(x)$ is equal to the slope found in step 1.

3x2−4x−33x2−4x−7(3x−7)(x+1)x=73=4=0=1x=−1$\begin{array}{rl}3x^2-4x-3& =4\\ 3x^2-4x-7& =0\\ (3x-7)(x+1)& =1\\ x=\frac{7}{3}& x=-1\end{array}$

The MVT guarantees that c∈(a,b)$c\in (a,b)$, and since 73∈(−1,4)$\frac{7}{3}\in (-1,4)$ this is the value we are looking for.

Note, the x=−1$x=-1$ is excluded since −1∉(−1,4)$-1\notin (-1,4)$.

Answer

x=73$x=\frac{7}{3}$ satisfies the MVT.

For reference, below is the graph of the function with one of the tangent lines and the secant line.

Shikhakaushal.blogspot.com
for video just go on downside link

https://youtu.be/Hn2dE4mArGU