matrices chapter 3 class 12 maths
For ClasMatrices Definition
Matrices for Class 12 Topics
The topics covered in matrices for class 12 include the following topics:
- Matrix Introduction
- Types
- Operations
- Transpose of a Matrix
- Symmetric and Skew Symmetric Matrix
- Elementary Operations of a Matrix (Transformations)
- Invertible Matrices
Matrix introduction
A matrix is a function which consists of an ordered rectangular array of numbers. The numbers in the array are called the entities or the elements of the matrix. The horizontal array of elements in the matrix is called rows, and the vertical array of elements are called the columns. If a matrix has m rows and n columns, then it is known as the matrix of order m x n.
Types of Matrices
Depending upon the order and elements, matrices are classified as,
Column Matrix
A column matrix is an m × 1 matrix, consisting of a single column of m elements. It is also called a column vector.
Row Matrix
A row matrix is a 1 × m matrix, consisting of a single row of m elements. It is also called a row vector.
Square Matrix
A matrix which has an equal number of rows and columns. It is expressed as m × m.
Diagonal Matrix
A matrix which has non-zero elements in its diagonal part running from upper left to the lower right or vice versa.
Scalar Matrix
The scalar matrix is a square matrix, which has all its diagonal elements equal and all the off-diagonal elements as zero.
Identity Matrix
A square matric which has all its principal diagonal elements as ones and all non-diagonal elements as zeros.
Zero Matrix
A matrix whose all entries are zero. It is also called a null matrix.
Equality of Matrices
Two matrices are said to be equal if-
(i) The order of both the matrices are the same
(ii) Each element of one matrix is equal to the corresponding element of the other matrix.
Matrices for Class 12 Examples
Example:
If ⎡⎣⎢x+3−6b−3z+4a−1−212y−700⎤⎦⎥=⎡⎣⎢0−62b+46−3−213y−22c+20⎤⎦⎥ , then find the value of a, b, c, x, y, and z.
Solution:
It is given that, the two matrices are equal. Therefore, the corresponding elements present in matrices should be equal to each other. By comparing the corresponding elements in the matrices, we get:
x+3 = 0.
⇒ x = -3
z +4 = 6
⇒ z = 6-4
⇒ z = 2
2y-7 = 3y-2
⇒3y-2y =-7+2
⇒y = -5
a-1 = -3
⇒a = -3+1
⇒a=-2
2c+2 = 0
⇒2c = -2
⇒ c = -1
b-3 = 2b+4
⇒2b-b = -3-4
⇒ b = -7
Therefore, the values of the variables are:
a = -2
b = -7
c = -1
x = -3
y = -5
z = 2
A matrix (plural: matrices) is an arrangement of numbers, expressions or symbols in a rectangular array. This arrangement is done in horizontal-rows and vertical-columns, having an order of number of rows x number of columns. Every pair of points in a Three-dimensional space represent a unique equation with one or more than one solution.
The basic idea or the central idea of applied mathematics revolves around Linear Algebra. For instance, by reliving the rules and regulations or rather say Axioms, we get into a generalization of vector space, which by calculus leads to the Solution of Differential Equations.
Algebra of Matrix
Algebra of matrix involves the operation of matrices, such as Addition, subtraction, multiplication etc.
Let us understand the operation of the matrix in a much better way-
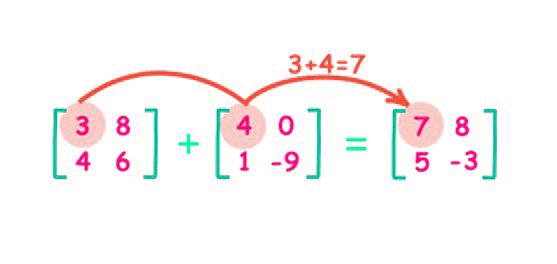
Addition/Subtraction of Matrices
Two matrices can be added/subtracted, iff (if and only if) the number of rows and columns of both the matrices are same, or the order of the matrices are equal.
For addition/subtraction, each element of the first matrix is added/subtracted to the elements present in the 2nd matrix.

Example:
Also, read:
Matrix Multiplication
Like Matrix can be Multiplied two ways,
(i) Scalar Multiplication
(ii) Multiplication with another matrix
- Scalar Multiplication – It involves multiplying a scalar quantity to the matrix. Every element inside the matrix is to be multiplied by the scalar quantity to form a new matrix.
For example-
- Multiplication of a matrix with another matrix:Two matrix can be multiplied iff the number of column of the first matrix is equal to the number of rows of the second matrix.
Consider two matrix M1 & M2, having order of m1×n1, and m2×n2, .
The matrices can be multiplied if and only if n1=m2 .

The matrices, given above satisfies the condition for matrix multiplication, hence it is possible to multiply those matrices.
The resultant matrix obtained by multiplication of two matrices, is the order of m1,n2 , where m1 is the number of rows in the 1st matrix and n2 is the number of column of the 2nd matrix.
Rule of Matrix Algebra
The algebra of matrix follows some rules for addition and multiplication. Let us consider A, B and C are three different square matrices. A’ is the transpose and A-1 is the inverse of A. I is the identity matrix and R is a real number.
Now as per the rules of laws of matrices:
Now as per the rules of laws of matrices:
- A+B = B+A →Commutative Law of Addition
- A+B+C = A +(B+C) = (A+B)+C →Associative law of addition
- ABC = A(BC) = (AB)C →Associative law of multiplication
- A(B+C) = AB + AC →Distributive law of matrix algebra
- R(A+B) = RA + RB
Also, see here rules for transposition of matrices:
- (A’)’ = A
- (A+B)’ = A’+B’
- (AB)’ = B’A’
- (ABC) = C’B’A’
The inverse rules of matrices are as follows:
- AI = IA = A
- AA-1 = A-1A = I
- (A-1)-1 = A
- (AB)-1 = B-1A-1
- (ABC)-1 = C-1B-1A-1
- (A’)-1 = (A-1)’
Solved Problems
Example 1: Given A=[3−1−57] and B=[1843] find A + B.
Solution:
Given,
A=[3−1−57] and B=[1843] Addition of A and B is:
A+B=[3−1−57]+[1843]=[3+1−1+8−5+47+3]=[47−110]
Given,
Example 2: If P=[5249] and Q=[1052] , then find P-Q.
Solution:
Given,
P=[5249] and Q=[1052] Subtraction of the matrices P and Q is:
A−B=[5249]−[1052]=[5−12−04−59−2]=[42−17]
Given,
Example 3: If A=[47−20] and B=[325−3] , then find the product of A and B.
Solution:
Given
A=[47−20] and B=[325−3] Product/multiplication of A and B is:
A×B=[47−20]×[325−3]=[4(3)+(−2)27(3)+0(2)4(5)+(−2)(−3)7(5)+0(−3)]=[12−42120+635]=[8212635]
Given
Matrix multiplication also known as matrix product is a binary operation that produces a single matrix by taking the two different matrices. We know that a matrix is an array of numbers. It consists of rows and columns. If you multiply a matrix by a scalar value, then it is known as scalar multiplication. An another case is that it is possible to multiply a matrix by another matrix. In this article, let us discuss how to multiply a matrix by another matrix, its algorithm, formula, 2×2 and 3×3 matrix multiplication with examples in detail.
Table of Contents:
Multiplying Matrices
Let’s learn how to multiply matrices.
Consider matrix A which is a × b matrix and matrix B which is a b ×c matrix.
Then matrix C = AB is defined as A × B matrix.
An element in matrix C, Cxy is defined as Cxy = Ax1By1 +….. + AxbBby = ∑bk=1 AxkBky for x = 1…… a and y= 1…….c
This is one of the most important topics in class 12. Matrices for class 12 explains the types of matrices in detail.
Matrix Multiplication Formula
Let’s take an example to understand this formula.
Let’s say A and B are two matrices, such that,
Then Matrix C = AB is denoted by
C = ⎡⎣⎢⎢⎢C11C12…….C1cC21C22…….C2c……………Ca1Ca2…….Cac⎤⎦⎥⎥⎥
An element in matrix C where C is the multiplication of Matrix A X B.
C = Cxy = Ax1By1 +….. + AxbBby = ∑bk=1 AxkBky for x = 1…… a and y= 1…….c
Now that you know what is matrix and how to multiply matrix, you can also understand other matrix operations like matrix addition etc.
2×2 Matrix Multiplication
Let’s consider a simple 2 × 2 matrix multiplication A = [3479] and another matrix B = [6528]
Now each of the elements of product matrix AB can be calculated as follows:
- AB11 = 3 × 6 + 7 ×5 = 53
- AB12 = 3 × 2 + 7 × 8 = 62
- AB21 = 4 × 6 + 9 × 5 = 69
- AB22 = 4 × 2 + 9 × 8 = 80
3×3 Matrix Multiplication
To understand the multiplication of two 3 × 3 matrices, let us consider two 3 × 3 matrices A and B.
Matrix A = ⎡⎣⎢1239817841410⎤⎦⎥ , Matrix B = ⎡⎣⎢567191583916⎤⎦⎥
Each element of the Product matrix AB can be calculated as follows:
- AB11 = 12×5 + 8×6 + 4×7 = 136
- AB12 = 12×19 + 8×15 + 4×8 = 380
- AB13 = 12×3 + 8×9+4×16 = 172
- AB21 = 3×5 + 17×6 + 14×7 = 215
- AB22 = 3×19 + 17×15 + 14×8 = 424
- AB23 = 3×3 + 17×9 + 14×16 = 386
- AB31 = 9×5 + 8×6 + 10×7 = 163
- AB32 = 9×19 + 8×15 + 10×8 = 371
- AB33 = 9×3 + 8×9 + 10×16 = 259
Therefore, Matrix AB = ⎡⎣⎢136215163380424371172386259⎤⎦⎥
Algorithm for Matrix Multiplication
There has been a significant amount of work in recent years in the field of matrix multiplication algorithms as it has found its application in many areas. There are four types of algorithms:
- Iterative Algorithm
- Divide and conquer algorithm
- Sub-cubic algorithms
- Parallel and distributed algorithms
This is majorly used in various programming languages such as C, Java, etc., for online multiplication. The most common are 2×2, 3×3 and 4×4, multiplication of matrices.
The operation is binary with entries in a set on which the operations of addition, subtraction, multiplication, and division are defined. These operations are the same as the corresponding operations on real and rational numbers.
Although there are many applications of matrices, essentially, multiplication of matrices is an operation in linear algebra. The linear mapping which includes scalar addition and multiplication is represented by matrix multiplication.
One can also find a wide range of algorithms on meshes. This type of algorithms is designed to minimize the inherent inefficiency of standard array algorithm where there can be a delay in the arrival of data from 2 different matrices.
Matrix Multiplication Example
Multiplication of 4×4 matrices is explained below with two 4×4 matrices A and B.
A = ⎡⎣⎢⎢⎢7414131482171512666394⎤⎦⎥⎥⎥ , B = ⎡⎣⎢⎢⎢5813671663144822944⎤⎦⎥⎥⎥
Following the same steps as in the previous 2 examples, we can construct AB matrix.
AB = ⎡⎣⎢⎢⎢378258370223381237497251286190346266224140277129⎤⎦⎥⎥⎥
A=⎡⎣⎢159261037114812⎤⎦⎥


The matrix in mathematics is a rectangular or square array of numbers or variables, arranged in the form of rows and columns. Individual items in a matrix are known as elements or entries.
The size of the matrix is determined by some its rows and columns. Matrix with ‘m’ rows and ‘n’ columns is read as ‘m*n’ matrix where m and n are its dimensions.
For example ,the matrix A mentioned above is a 3*4 matrix ,where 1,5,9,2,6 etc are its elements.
Matrix Operations
Two matrices can be added or subtracted element by element, provided both are of the same size.
Below image will help us in understanding the addition and subtraction operation on matrices,


But there is a rule for matrix multiplication, the number of columns in the first matrix should be equal to a number of rows in the second.
If A is a matrix of m*n and B is a matrix of n*p then their product matrix C=(A*B) will be m*p, whose elements are produced by the dot product of a corresponding row of A and a corresponding column of B.

The above image gives us a better understanding of multiplication of matrices.
Applications of Matrices in Various Fields
- Cryptography: Cryptography is a practice of hiding information for security purposes. Suppose you have a confidential data which has to be sent to someone. you can use a matrix to make the information to be readable to only the recipient.
- Fourier analysis
- Gauss theorem
- Finding electric currents using matrix equations
- Finding forces in the bridge
This is all about the introduction to matrices and its application in the engineering field.
By Shikha Kaushal
