CHAPTER - 2 (Polynomials)

A polynomial is an expression consists of constants, variables and exponents. It’s mathematical form is-

a_nxⁿ + a_n-1x^n-1 + a_n-2x^n-2 + a₂x² + a₁x + a₀ = 0

where the (a_i)’s are constant

Degree of Polynomials

The highest power of x in polynomial p(x) is called the degree of the polynomial p(x).

Note: Exponents of variables of a polynomial .i.e. degree of polynomials should be whole numbers.

In Algebra "Degree" is sometimes called "Order"
The Degree (for a polynomial with one variable, like x) is:

the largest exponent of that variable.

More Examples:

4x		The Degree is 1 (a variable without an exponent actually has an exponent of 1)

4x³ − x + 3		The Degree is 3 (largest exponent of x)

x² + 2x⁵ − x		The Degree is 5 (largest exponent of x)

z² − z + 3		The Degree is 2 (largest exponent of z)

Types of Polynomial according to their Degrees

Type of polynomial	Degree	Form
Constant	0	P(x) = a
Linear	1	P(x) = ax + b
Quadratic	2	P(x) = ax² + ax + b
Cubic	3	P(x) = ax³ + ax² + ax + b
Bi-quadratic	4	P(x) = ax⁴ + ax³ + ax² + ax + b

Value of Polynomial

Let p(y) is a polynomial in y and α could be any real number, then the value calculated after putting the value y = α in p(y) is the final value of p(y) at y = α. This shows that p(y) at y = α is represented by p (α).

Solving Polynomials

A polynomial looks like this:

example of a polynomial

Solving

"Solving" means finding the "roots" ...

... a "root" (or "zero") is where the function is equal to zero:

In between the roots the function is either entirely above,
or entirely below, the x-axis

Example: −2 and 2 are the roots of the function x² − 4

Let's check:

when x = −2, then x² − 4 = (−2)² − 4 = 4 − 4 = 0
when x = 2, then x² − 4 = 2² − 4 = 4 − 4 = 0

How do we solve polynomials? That depends on the Degree!

Degree

The first step in solving a polynomial is to find its degree.
The Degree of a Polynomial with one variable is ...

... the largest exponent of that variable.

When we know the degree we can also give the polynomial a name:

Degree	Name	Example	Graph Looks Like
0	Constant	7
1	Linear	4x+3
2	Quadratic	x²−3x+2
3	Cubic	2x³−5x²
4	Quartic	x⁴+3x−2	...
etc	...	...	...

Zero of a Polynomial

If the value of p(y) at y = k is 0, that is p (k) = 0 then y = k will be the zero of that polynomial p(y).

Geometrical meaning of the Zeroes of a Polynomial

Zeroes of the polynomials are the x coordinates of the point where the graph of that polynomial intersects the x-axis.

Graph of a Linear Polynomial

Graph of a linear polynomial is a straight line which intersects the x-axis at one point only, so a linear polynomial has 1 degree.

Example: 2x+1

2x+1 is a linear polynomial:

The graph of y = 2x+1 is a straight line

It is linear so there is one root.
Use Algebra to solve:

A "root" is when y is zero: 2x+1 = 0

Subtract 1 from both sides: 2x = −1

Divide both sides by 2: x = −1/2

And that is the solution:

x = −1/2

Graph of Quadratic Polynomial

Case 1: When the graph cuts the x-axis at the two points than these two points are the two zeroes of that quadratic polynomial.

Case 2: When the graph cuts the x-axis at only one point then that particular point is the zero of that quadratic polynomial and the equation is in the form of a perfect square

Case 3: When the graph does not intersect the x-axis at any point i.e. the graph is either completely above the x-axis or below the x-axis then that quadratic polynomial has no zero as it is not intersecting the x-axis at any point.

Hence the quadratic polynomial can have either two zeroes, one zero or no zero. Or you can say that it can have maximum two zero only

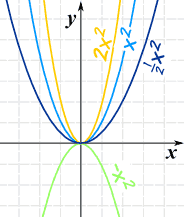
Graphing Quadratic Equations

A Quadratic Equation in Standard Form
(a, b, and c can have any value, except that a can't be 0.)

Here is an example:

Graphing

You can graph a Quadratic Equation using the Function Grapher, but to really understand what is going on, you can make the graph yourself. Read On!

The Simplest Quadratic

The simplest Quadratic Equation is:

f(x) = x²

And its graph is simple too:

This is the curve f(x) = x²
It is a parabola.

Now let us see what happens when we introduce the "a" value:

f(x) = ax²

Larger values of a squash the curve inwards
Smaller values of a expand it outwards
And negative values of a flip it upside down

Relationship between Zeroes and Coefficients of a Polynomial

Polynomials can be linear (x), quadratic (x²), cubic (x³) and so on, depending on the highest power of the variable.
The number of zeroes of a polynomial is equal to the degree of the polynomial, and there is a well-defined mathematical relationship between the zeroes and the coefficients. Mathematically, if p(x) is a polynomial in x, and if k is any real number, then the value obtained by replacing x by k in p(x) is called the value of p(x) at x = k and is denoted by p(k).
Here, the real number k is said to be a zero of the polynomial of p(x), if p(k) = 0.
Simply put, the zeroes of a polynomial function are the solutions to the equation you get, when you set the polynomial equal to zero.
Let us understand the difference between zeros and roots in a polynomial equation.

A zero is a value for which a polynomial is equal to zero.
- When you set a polynomial equal to zero, then you have a polynomial equation where the equations roots are same as the polynomial’s zeroes.
A root is a value for which a polynomial equation is true.
Example: The polynomial x-5 has one zero, that is x = 5. And the polynomial equation x-5 = 0 has one root, that is, x = 5.

The number of zeroes of a polynomial is equal to the degree of the polynomial, and there is a well-defined mathematical relationship between the zeroes and the coefficients.

Linear Polynomial

Any equation of the first degree is known as a linear equation. It is an equation of the form ax+b = 0, where and b are constants and x is a variable.
The general form of a linear polynomial is p(x) = ax+b, its zero is

\frac{- b}{a}

\frac{- (c o n s t a n t t e r m)}{(c o e f f i c i e n t o f x)}

Quadratic Polynomial

General form of a quadratic polynomial is ax² + bx + c where a ≠ 0. There are two zeroes, say

α

and

β

of a quadratic polynomial, where

Sum of the roots = $α + β =$

\frac{- b}{a}

\frac{- (c o e f f i c i e n t o f x)}{(c o e f f i c i e n t o f x^{2})}

Product of the toots =

α β =

\frac{c}{a}

\frac{(c o e f f i c i e n t o f x)}{(c o e f f i c i e n t o f x^{2})}

Division Algorithm for Polynomial

If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that

P(x) = g(x) × q(x) + r(x),

where r(x) = 0 or degree of r(x) < degrdee of g(x).

by shikha kaushal

Search This Blog

Shikhakaushal

chapter 2 polynomial class 10 cbse