Relations And Functions For Class 11
NOTES OF CHAPTER 1 (RELATION and FUNCTION)
RELATION AND FUNCTION
“Relations and Functions” is one of the most important topics in algebra. Relations and functions – these are the two different words having different meaning mathematically. You might get confused about their difference. Before we go deeper, let’s understand the difference between both with a simple example.
An ordered pair, represents as (INPUT, OUTPUT):
Relation shows the relationship between INPUT and OUTPUT. Whereas
A function is a relation which derives one OUTPUT for each given INPUT.
Note: All functions are relations, but not all relations are functions.

In this section, you will find the basics of the topic – definition of functions and relations, Special functions, different types of relations and some of the solved examples.
What is a Function?
A function is a relation which describes that there should be only one output for each input. OR we can say that, a special kind of relation(a set of ordered pairs) which follows a rule i.e every X-value should be associated to only one y-value is called a Function.
For example:
| Domain | Range |
| -1 | -3 |
| 1 | 3 |
| 3 | 9 |
Let us also look at the definition of Domain and Range of a function.
| Domain | It is a collection of the first values in the ordered pairs (Set of all input (x) values). |
| Range | It is a collection of the second values in the ordered pairs (Set of all output (y) values). |
Example:
In the relation, {(-2, 3), {4, 5), (6, -5), (-2, 3)},
The domain is {-2, 4, 6} and Range is {-5, 3, 5}.
Note: Don’t consider duplicates while writing Domain and Range and also write it in increasing order.
Types of Functions
In terms of relations, we can define the types of functions as:
- One to one function or Injective function: A function f: P → Q is said to be One to One if for each element of P there is a distinct element of Q.
- Many to one function: A function which maps two or more elements of P to the same element of set Q.
- Onto Function or Surjective function: A function for which every element of set Q there is pre-image in set P
- One-one and Onto function or Bijective function: The function f matches with each element of P with a discrete element of Q and every element of Q has a pre-image in P.
Read here:
Special Functions in Algebra
There are some of the important functions as follow:
- Constant Function
- Identity Function
- Linear Function
- Absolute Value Function
- Inverse Functions
What is the Relation?
It is a subset of the Cartesian product. Or simply, a bunch of points(ordered pairs).
Example: {(-2, 1), (4, 3), (7, -3)}, usually written in set notation form with curly brackets.
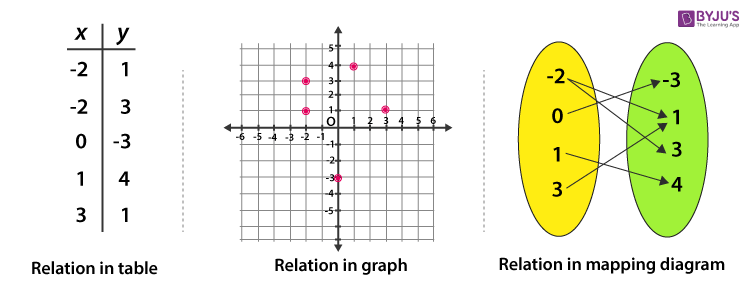
Relation Representation
There are other ways too to write the relation, apart from set notation such as through tables, plotting it on XY- axis or through mapping diagram.
Types of Relations
Different types of relations are as follows:
- Empty Relations
- Universal Relations
- Identity Relations
- Inverse Relations
- Reflexive Relations
- Symmetric Relations
- Transitive Relations
Let us discuss all the types one by one.
Empty Relation
When there’s no element of set X is related or mapped to any element of X, then the relation R in A is an empty relation also called as void. I.e R= ∅.
For example,
if there are 100 mangoes in the fruit basket. There’s no possibility of finding a relation R of getting any apple in the basket. So, R is Void as it has 100 mangoes and no apples.
Universal relation
R is a relation in a set, let’s say A is a universal Relation because, in this full relation, every element of A is related to every element of A. i.e R = A × A.
It’s a full relation as every element of Set A is in Set B.
Identity Relation
If every element of set A is related to itself only, it is called Identity relation.
I={(A, A), ∈ a}.
For Example,
When we throw a dice, the outcome we get is 36. I.e (1, 1) (1, 2), (1, 3)…..(6, 6). From these, if we consider the relation(1, 1), (2, 2), (3, 3) (4, 4) (5, 5) (6, 6), it is an identity relation.
Inverse Relation
If R is a relation from set A to set B i.e R ∈ A X B. The relation R−1 = {(b,a):(a,b) ∈ R}.
For Example,
If you throw two dice if R = {(1, 2) (2, 3)}, R−1 = {(2, 1) (3, 2)}. Here the domain is the Range R−1 and vice versa.
Reflexive Relation
A relation is a reflexive relation If every element of set A maps to itself. I.e for every a ∈ A,(a, a) ∈ R.
Symmetric Relation
A symmetric relation is a relation R on a set A if (a,b) ∈ R then (b, a) ∈ R, for all a &b ∈ A.
Transitive Relation
If (a,b) ∈ R, (b,c) ∈ R, then (a,c) ∈ R, for all a,b,c ∈ A and this relation in set A is transitive.
Equivalence Relation
If and only if a relation is reflexive, symmetric and transitive, it is called an equivalence relation.
How to convert a Relation into a function?
A special kind of relation(a set of ordered pairs) which follows a rule i.e every X-value should be associated with only one y-value is called a Function.
Examples
Example 1: Is A = {(1, 5), (1, 5), (3, -8), (3, -8), (3, -8)} a function?
Solution: If there are any duplicates or repetitions in the X-value, the relation is not a function.
But there’s a twist here. Look at the following example:

Though X-values are getting repeated here, still it is a function because they are associating with the same values of Y.
The point (1, 5) is repeated here twice and (3, -8) is written thrice. We can rewrite it by writing a single copy of the repeated ordered pairs. So, “A” is a function.
Example 2: Give an example of an Equivalence relation.
Solution:
If we note down all the outcomes of throwing two dice, it would include reflexive, symmetry and transitive relations. that will be called an Equivalence relation.
Example 3: All functions are relations, but not all relations are functions. Justify.
Solution:
Let’s suppose, we have two relations given in below table
| A relation which is not a function | A relation that is a function |
 |  |
| As we can see duplication in X-values with different y-values, then this relation is not a function. | As every value of X is different and is associated with only one value of y, this relation is a function |
