CBSE Notes Class 12 Maths Inverse Trigonometric Functions

-


CBSE Notes Class 12 Maths Inverse Trigonometric Functions


Inverse Function
If y = f(x) and x = g(y) are two functions such that f (g(y)) = y and g (f(y)) = x, then f and y are said to be inverse of each other
i.e., g = f-1
IF y = f(x), then x = f-1(y)
Inverse Trigonometric Functions
If y = sin X-1, then x = sin-1 y, similarly for other trigonometric functions.
This is called inverse trigonometric function .
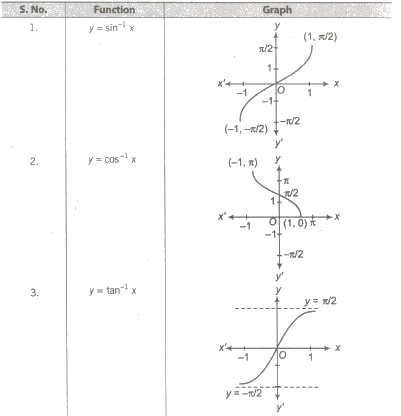
Now, y = sin-1(x), y ∈ [π / 2 , π / 2] and x ∈ [-1,1].
(i) Thus, sin-1x has infinitely many values for given x ∈ [-1, 1].
(ii) There is only one value among these values which lies in the interval [π / 2 , π / 2]. This value is called the principal value.
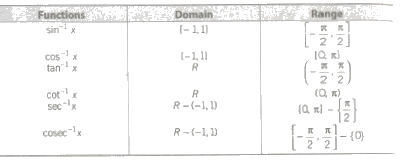
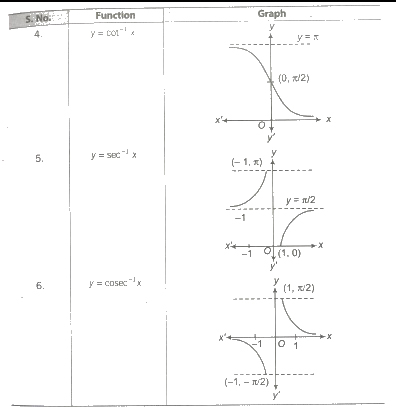
Domain and Range of Inverse Trigonometric FunctionsGraphs of Inverse Trigonometric Functions
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
Properties of Inverse Trigonometric Functions
Property I
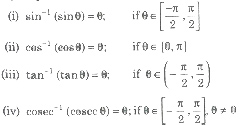
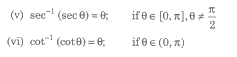
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
Property II
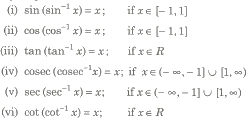
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
Property III
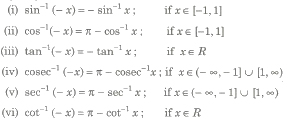
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
Property IV
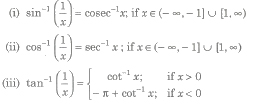
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
Property V
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
Property VI
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
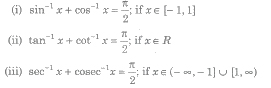
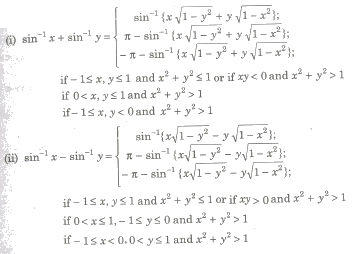
Property VII
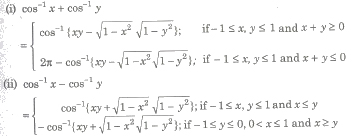
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
Property VIII
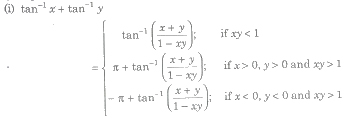
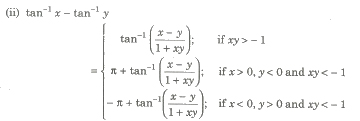
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
Property IX
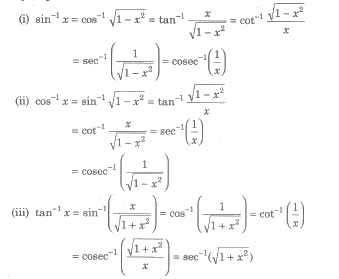
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
Property X
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
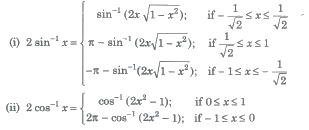
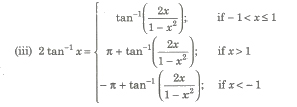
Property XI
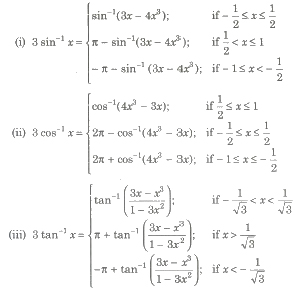
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
Property XII
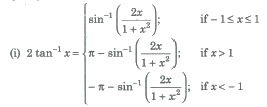
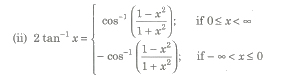
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
Important Results
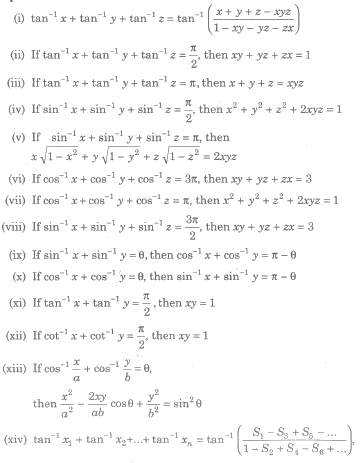
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
where Sk denotes the sum of the product of x1,x2,…xn takes k at a time.
Inverse Hyperbolic Functions
If sinh y = x, then y is called the inverse hyperbolic sine of x and it is written as y = sinh-1 x.
Similarly, cosh-1 x, tan h-1 x etc., can be defined,
Domain and Range of Inverse Hyperbolic Functions
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
Relation between Inverse Circular Functions and Inverse Hyperbolic Functions
(i) sinh-1x = – i sin-1(ix)
(ii) cosh-1x = – i cos-1 x .
(iii) tanh--1x = – i tan-1(ix)
Important Results
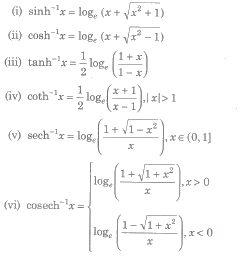
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
Trigonometric Equation
An equation involving one or more trigonometrical ratios of unknown angle is called a trigonometric equation .
Solution/Roots of a Trigonometric Equation
A value of the unknown angle which satisfies the given equation, is called a solution or root of the equation.
The trigonometric equation may have infinite number of solutions.
(i) Principal Solution – The least value of unknown angle which satisfies the given equation, is called a principal solution of trigonometric equation.(ii) General Solution – We know that, trigonometric function are periodic and solution of trigonometric equations can be generalised with the help of the periodicity of the trigonometric functions. The solution consisting of all possible solutions of a trigonometric equation is called its general solution.

Important Results
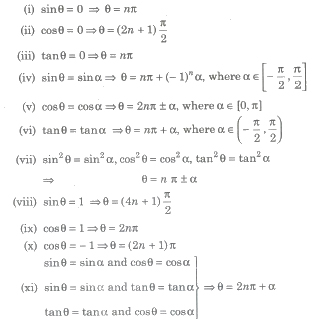
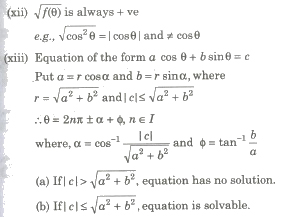
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
CBSE Class 11 and 12 Maths Notes Inverse T - Functions and T - Equations
Important Points to be Remembered
(i) While solving an equation, we have to square it, sometimes the resulting roots does not satisfy the original equation.
(ii) Do not cancel common factors involving the unknown angle on LHS and RHS.Because it may be the solution of given equation.
(iii) (a) Equation involving sec θ or tan θ can never be a solution of the form (2n + 1) π / 2.
(b) Equation involving coseca or cote can never be a solution of the form θ = nπ.
For Class 11
Location: Delhi, India

Popular posts from this blog

Compound Interest class 8 chapter6(notes) maths definition, formula

-
Image
Compound Interest Definition Compound interest is the interest calculated on the principal and the interest accumulated over the previous period. It is different from the simple interest where interest is not added to the principal while calculating the interest during the next period. Compound interest finds its usage in most of the transactions in the banking and finance sectors and also in other areas as well. Some of its applications are: Increase or decrease in population. The growth of bacteria. Rise or depreciation in the value of an item. Compound Interest Formula The compound interest formula is given below: Compound Interest = Amount – Principal Where the  amount  is given by: Where, A= amount P= principal R= rate of interest n= number of times interest is compounded per year It is to be noted that the above formula is the general formula for the number of times the principal is compounded in an year. If the amount is compounded annually, the amount is given as- ...
Read more

Revision notes for class 10 & 9 CIRCLES

-
Image
Revision Notes on Circle The equation of a   circle   with its center at C(x 0 , y 0 ) and radius r is: (x – x 0 ) 2  + (y – y 0 ) 2  = r 2     If x 0  = y 0  = 0 (i.e. the centre of the circle is at origin) then  equation of the circle   reduce to x 2  + y 2  = r 2 . If r = 0 then the circle represents a point or a point circle. The equation x 2  + y 2  + 2gx + 2fy + c = 0 is the general equation of a circle with centre (–g, –f) and radius √(g 2 +f 2 -c). Equation of the circle with points P(x 1 , y 1 ) and Q(x 2 , y 2 ) as extremities of a diameter is (x – x 1 ) (x – x 2 ) + (y – y 1 )(y – y 2 ) = 0.  For general circle, the equation of the chord is x 1 x + y 1 y + g(x 1  + x) + f(y 1  +y) + c = 0 For circle x 2  + y 2  = a 2 , the equation of the chord is x 1 x + y 1 y = a 2   The equation of the  chord  AB (A ≡ (R cos α, R sin α);...
Read more

Basic concept of probability

-
Image
Important Formulas - Probability or Chance Probability or Chance Probability or chance is a common term used in day-to-day life. For example, we generally say, 'it may rain today'. This statement has a certain uncertainty. Probability is quantitative measure of the chance of occurrence of a particular event. Experiment An experiment is an operation which can produce well-defined outcomes. Random Experiment If all the possible outcomes of an experiment are known but the exact output cannot be predicted in advance, that experiment is called a random experiment. Examples Tossing of a fair coin When we toss a coin, the outcome will be either Head (H) or Tail (T) Throwing an unbiased die Die is a small cube used in games. It has six faces and each of the six faces shows a different number of dots from 1 to 6. Plural of die is dice. When a die is thrown or rolled, the outcome is the number that appears on its upper face and it is a random in...
Read more